Linear Regression from Scratch. I’m starting off the series with one of… | by Perrin Alaine-Sedano | Jun, 2024

I’m starting off with one in every of many best machine learning strategies: linear regression. The mathematical part of this submit requires an excellent working data of linear algebra and calculus to adjust to, which might be the case for the rest of the sequence. That’s unavoidable since these subjects underpin an infinite amount of machine learning and are situations for a deep understanding. With that talked about, let’s dive in.

Linear regression is the responsibility of taking a sequence of things and discovering a line of best match. Sooner than we’re in a position to decide discover ways to uncover a line of best match, we now have to understand what that basically means.

We are going to intuitively inform that the highway in Decide 1 is a better match to the data elements than say, this one:

Why? Because of the elements in Decide 2 are farther away from the highway than these in Decide 1. Let’s decide discover ways to mathematically formalize this intuition so we’re in a position to define precisely what “best match” means.

Let’s start off in two dimensions. On this case, data elements are (x, y) pairs and might be merely visualized on a graph similar to the figures above. We have to uncover a linear function f(x) = kx which best represents the data. Phrase that this model assumes a line that passes by way of the origin. We acquired’t ponder the chance of an intercept aside from the origin however (we’ll get to that shortly).

Say we now have now a bunch of n data elements,

For each x-value, we’re ready to make use of our model to accumulate a predicted y-value. This case, with only one unbiased variable (x) and one dependent variable (y) known as simple linear regression. I’ll use a chief picture to tell apart the anticipated y values from the exact y-values. So, the model’s predicted y-value for a given x-value is given by the parts

Now let’s put all the x values proper right into a vector, and the y values into one different vector.

That is called vectorization, and has a complete lot of benefits for points in data science. Combining a complete lot of explicit individual values into vectors makes mathematical formulation far more compact and less complicated to objective about. Vectorization in code moreover normally improves effectivity. It’s so much faster to hold out vector arithmetic on an enormous array of values than to endure using a for loop and performance on each one after the other. Many numerical computing libraries like Numpy allow doing vector arithmetic very fast. It moreover permits for parallelization with {{hardware}} like GPUs, the place operations are carried out concurrently to completely totally different elements of an array. As quickly as as soon as extra, this wouldn’t be potential using a loop, the place each operation should happen one after the alternative.

We are going to moreover create a vector containing all of our predicted y-values:

In order to find the highway of best match, we now have to know how far y’ is from the vector of exact values, y. We are going to check out the excellence of the two vectors: y’ — y. Nonetheless, this generally is a vector and we want a single amount representing the error of the model. We’re going to make use of sum-of-squares error (SSE), which equal to ||y’ — y||², the squared magnitude of the excellence vector. It’s often called “sum-of-squares” because of it’s equal to the sum of the squared entries of y’ — y:

As for why we use ||y’ — y||² as a substitute of merely ||y’ — y||, one reply is that squared magnitude is just so much simpler to work with. ||y’ — y|| has an extra sq. root picture outdoor the summation:

This is ready to make working with the parts a LOT further tedious when taking derivatives, as an illustration.

Now that we’ve outlined the error of a linear regression model, we now have to discover ways to cut back it. Let’s enhance out the expression for SSE.

If we substitute in okayx for y’ as per Equation 1, we get

We now have to find the price of okay that minimizes the error when x and y are held mounted. To take motion, we’re in a position to set the by-product of Expression 1 w.r.t. okay to zero and treatment:

This offers us the price of okay which minimizes the sum-of-squares error. Armed with this data, we’re in a position to code a SimpleLinearRegressor. It’ll have just one event variable — the slope, okay.

class SimpleLinearRegressor:
"""Performs simple linear regression."""
def __init__(self):
self.okay = None

It’ll have a predict approach that takes a amount or array of numbers as a parameter and offers a prediction or array of predictions consequently.

def predict(self, x):
"""
Presents predicted y-values from an enter x-value, or vector of x-values.
:param x: The enter value(s).
:return: The anticipated y-value(s).
"""
if self.okay is None:
enhance RegressionModelNotFitError('Oh no! The model has not been match!')
return self.okay * x

It’ll moreover desire a match approach that finds the proper value of okay primarily based totally on the x and y vectors using Equation 2. That’s the true guts of the class.

def match(self, x, y):
"""
Fits the model primarily based totally on the given vectors of x and y values.
:param x: A vector of x-values.
:param y: A vector of y-values.
:return: The sum-of-squares error of the fitted model.
"""
self.okay = x @ y / (x @ x)
diff = self.predict(x) - y
return diff @ diff

We should at all times generate some data to examine the model. I’ll create a function that generates a vector of random x-values inside a spread, computes corresponding y-values using a linear model, after which offers Gaussian noise to those y-values.

def generate_noisy_data(n_points, slope, x_range, noise_stddev):
"""
Generates 2nd data elements primarily based totally on a linear relationship with added Gaussian noise.
:param n_points: The number of data elements to generate.
:param slope: The slope of the highway.
:param x_range: The differ from which to draw x-values.
:param noise_stddev: The standard deviation of the Gaussian noise in order so as to add to each y-value.
:return: Vectors of x and y values.
"""
x = np.random.uniform(*x_range, n_points)
y = slope * x + np.random.common(scale=noise_stddev, dimension=n_points)
return x, y

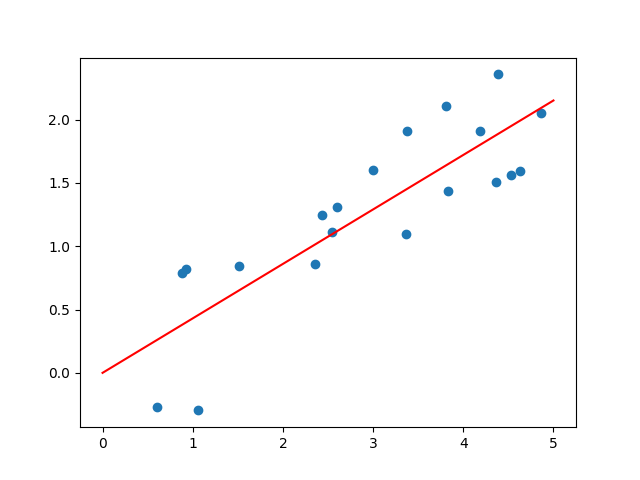
Let’s see how correctly the SimpleLinearRegressor can get nicely the distinctive slope from the randomized data. I’ll use matplotlib for visualization.

x_range = np.array([0, 5])
x, y = generate_noisy_data(n_points=20, slope=0.42, x_range=x_range, noise_stddev=0.5)
plt.scatter(x, y)
regressor = SimpleLinearRegressor()
match = regressor.match(x, y)
slope = regressor.okay
plt.plot(x_range, [0, 2 * x_range[1]], shade="crimson")
plt.textual content material(3, 0, f'Error: {"{:.2f}".format(match)}nPredicted slope: {"{:.2f}".format(slope)}')
plt.current()

Proper right here’s the output of 1 run:

As you might even see, it does an exquisite job! The slope predicted by the regression model is identical because the slope enter of generate_noisy_data to at least 2 decimal areas.

We’ve seen discover ways to perform linear regression with just one unbiased variable x, and one dependent variable, y. Now let’s suppose that y is decided by m unbiased variables, so we’re working with (m + 1)-dimensional data. We’d have n data elements which look like this:

Proper right here x_ij denotes value of the jth unbiased variable inside the ith data degree.

Consolidating our data by way of vectorization is always an excellent first step.

We are going to collect all the y-values proper right into a vector as sooner than:

Nonetheless, now that our x data has two indices, using a vector for the xs is not ideally suited. As an alternative we’re in a position to collect them proper right into a matrix the place each row is a single data degree:

I’ll use capital X_ij and lowercase x_ij any extra interchangeably to seek the advice of with entries on this matrix.

The linear model which we’re making an attempt to go well with to our data now appears to be considerably further subtle:

We now have m coefficients, or “slopes”, one for each unbiased variable, denoted by βs.

We are going to make a vector of each data degree

The matrix X might be thought of having each of these vectors as its rows:

Let’s moreover make a vector of all the β coefficients

Equation 3 can then be expressed very concisely as

Nonetheless, we’re in a position to get far more concise by combining the equations for each predicted value y’_i proper right into a vector of all of the anticipated values.

Similar to in simple linear regression, we’ll be making an attempt to scale back the sum-of-squares error ||y’ — y||²

Using Equation 4 we’re in a position to enhance out the parts in relation to X, y, and β.

Look acquainted? It’s masses similar to the parts for error in simple linear regression. We now have to find the price of β which minimizes it. First discover that the ||y||² time interval is irrelevant as a result of it doesn’t depend on β, so we’re really making an attempt to scale back

We’d stop proper right here since Numpy has a numpy.linalg.lstsq approach which may uncover the proper value of β with merely X and y as enter. Whereas technically not in direction of my rule of solely using Python and Numpy for computations, this feels an extreme quantity of like dishonest in a submit about “linear regression from scratch.” As an alternative, I’m going to dive into some math.

In order to find β which is ready to lower Expression 2, we should at all times set its gradient w.r.t. β equal to zero and treatment. To do this, we’ll convert Expression 2 into componentwise variety after which take the by-product w.r.t each component of β individually.

Using the componentwise parts for the dot product,

and for matrix-vector multiplication,

we’re in a position to convert Expression 2 to componentwise variety:

Now let’s take the by-product of Expression 3 w.r.t. a selected component of β, β_l:

To simplify Expression 4, we’ll should take the by-product of two summations:

and

Let’s take care of each of them individually.

Expression 5 By-product

Expression 5 might be expanded out as:

In English, this means “the half the place neither j nor okay is identical as l, plus the half the place okay is identical as l nonetheless j simply isn’t, plus the half the place j is identical as l nonetheless okay simply isn’t, plus the half the place j and okay are every equal to l.” Since every j and okay ought to each be equal to or not equal to l, these 4 sums cowl all prospects. All of them collectively thus equal the distinctive summation of Expression 5.

Uncover that the two heart sums in Expression 7 are comparable apart from the title of an index variable (j vs okay). Given that title is unfair and we’d merely as merely rename the index variable inside the third sum to j, these two sums have the an identical value. Thus the expression might be rewritten as

Now we’re in a position to take the by-product:

Phrase that the first time interval turns into zero as a result of it doesn’t comprise a β_l.

Expression 6 By-product

Discovering the by-product of Expression 6 is means simpler:

Proper right here as quickly as as soon as extra we break up the second summation right into a element containing β_l and a element not containing β_l. The latter is zeroed out all through differentiation.

Inserting it All Collectively

Now let’s substitute the derivatives we merely found, Expressions 8 and 9, once more into Expression 4 and simplify. We are going to then convert once more from componentwise variety to vector variety.

At this degree we’re ready to make use of the identification

to transform Equation 5 extra:

And we’re carried out! Any β for which the gradient of the error is zero ought to obey Equation 6.

It’s potential you’ll be questioning whether or not or not setting the gradient to zero like that can be a respectable strategy of discovering an optimum decision. In any case, this would possibly merely uncover a local minimal fairly than the worldwide minimal. Fortuitously, linear regression is a convex optimization draw back. This math stack exchange answer presents a proof. An mandatory property of a convex optimization draw back is that any native minimal may also be a world minimal, so there’s nothing to stress about.

Now that we’re assured of our decision’s correctness, we now have to treatment Equation 6 for β. Numpy presents a numpy.linalg.treatment function, nevertheless it certainly solely works if the equation has just one decision. Another option might be altering the matrix to diminished row echelon variety, nonetheless significantly surprisingly Numpy doesn’t have a utility for this. After some digging I discovered numpy.linalg.qr, which performs QR factorization of an enter matrix. An answer on math stack exchange and its suggestions have been instrumental in serving to me uncover methods to make use of QR factorization for equation fixing.

If we have to treatment the linear equation Ax = b the place A is a sq. matrix (discover that X^TX need to be sq.), we’re in a position to start by discovering an orthonormal sq. matrix Q and an larger triangular matrix R such that QR = A. The equation Ax = b turns into QRx = b. Since Q need to be invertible, the equation is also extra reworked into Rx = Q^-1b. R is larger triangular and the exact facet is just a vector, so all I really want is the flexibleness to resolve Uv = w the place U is an larger triangular matrix.

I created a function, solve_upper_triangular, to hold out the responsibility. I acquired’t go into an extreme quantity of component about its workings since this submit isn’t about discover ways to treatment linear equations, nonetheless primarily it begins on the ultimate row of the matrix and works backwards, at each row substituting in any beforehand set values for variables. It then assigns the price 1 to all nonetheless one in every of many remaining variables with nonzero coefficients inside the row and solves for that final variable in relation to all the others.

def solve_upper_triangular(a, b):
"""
Solves the linear equation ax = b for x.
:param a: An n x n larger triangular matrix.
:param b: An n-dimensional vector.
:return: A vector x for which ax = b.
"""
tracker = np.zeros(a.kind[1])
end result = np.zeros(a.kind[1])
for row, val in zip(a[::-1], b[::-1]):
unset_var_indices = np.the place((tracker == 0) & (row != 0))[0]
if len(unset_var_indices) == 0:
if np.isclose(end result @ row, val):
proceed
else:
enhance UnsolvableError('The given values of a and b result in an unsolvable equation.')
tracker[unset_var_indices] = 1
end result[unset_var_indices[1:]] = 1
i = unset_var_indices[0]
end result[i] = (val - end result @ row) / row[i]
return end result

I’m now in a position to create a MultipleLinearRegressor.

class MultipleLinearRegressor:
"""Performs various linear regression."""
def __init__(self):
self.beta = None

Similar to the SimpleLinearRegressor, it will probably have a predict approach and a match approach.

The earlier merely calculates the matrix product between a matrix X or vector x and β.

def predict(self, x):
"""
Presents predicted y-values from a given array of x-values.
:param x: Vector or matrix of x-values.
:return: Vector of predicted y-values.
"""
if self.beta is None:
enhance RegressionModelNotFitError('Oh no! The model has not been match!')
return x @ self.beta

The match approach solves Equation 6 by QR factorizing X^TX after which using solve_upper_triangular to hunt out the reply of Rβ = Q^-1X^Ty. It moreover returns the sum of squares error for the fitted model.

def match(self, x, y):
"""
Fits the model primarily based totally on a matrix of x-values and vector of corresponding y-values.
:param x: Matrix of x-values.
:param y: Vector of y-values.
:return: The sum-of-squares error of the fitted model.
"""
x_t = x.transpose()
q, r = np.linalg.qr(x_t @ x)
vec = np.linalg.inv(q) @ x_t @ y
self.beta = solve_upper_triangular(r, vec)
diff = self.predict(x) - y
return diff @ diff

Let’s see how the MultipleLinearRegressor performs. I’ll create a generate_noisy_data function much like the sooner one nonetheless which takes a vector β of parameters and generates a matrix X and vector y of data elements, then offers Gaussian noise to the y-values as sooner than.

def generate_noisy_data(n_data_points, n_independent_variables, beta, x_range, noise_stddev):
"""
Generates data elements primarily based totally on a linear relationship with added Gaussian noise.
:param n_data_points: The number of data elements to generate.
:param n_independent_variables: The number of unbiased variables in each data degree.
:param beta: The vector of coefficients for the unbiased variables.
:param x_range: The differ from which to draw x-values.
:param noise_stddev: The standard deviation of the Gaussian noise in order so as to add to each y-value.
:return: Matrix of x-values and vector of y-values.
"""
x = np.random.uniform(*x_range, (n_data_points, n_independent_variables))
y = x @ beta + np.random.common(scale=noise_stddev, dimension=n_data_points)
return x, y

Now generate some data and see how correctly the regressor recovers the distinctive β.

regressor = MultipleLinearRegressor()
x, y = generate_noisy_data(n_data_points=500,
n_independent_variables=10,
beta=np.array([-10, 5, -8, -2, 1, -3, 4, -5, -1, 3]),
x_range=np.array([-100, 100]),
noise_stddev=50)
sse = regressor.match(x, y)
print(f'Sum Squared Error: {sse}')
print(f'Beta: {regressor.beta}')

The output from one run is

Sum Squared Error: 1259196.6403705715
Beta: [-9.95436533  5.02469925 -7.95431319 -1.97266714  1.03726794 -2.95935233
4.03854255 -4.98106051 -1.01840914  3.0410695]

As we’re in a position to see it does a reasonably good job of getting close to the distinctive parameter values.

What about Bias?

To this point I’ve solely talked about regression fashions with a y-intercept of zero. Nonetheless, this may not be an excellent match for all data. What if we want a model like f(x) = x⋅β + b, the place b is a number of nonzero mounted? The price b is usually often called a bias inside the context of machine learning, as a result of it “biases” the data in route of a specific value even when all the model’s inputs are zero.

I’ve left this consideration for a quick addendum because of it appears together with bias in regression fashions doesn’t require so much effort: It’s equal to together with an extra unbiased variable to the data which always takes the price 1. For example, if we had some two dimensional data and wanted in order so as to add bias to our regressor, as a substitute of changing into a model of the form f(x) = kx, we’d match the model

The variable x_1 would signify our distinctive data, and x_2 might be set equal to 1 in every datapoint. A datapoint (x, y) would thus turn into (x_1, x_2, y) = (x, 1, y). Plugging in x_1 = x and x_2 = 1, Equation 7 reduces to

Proper right here β_1 is the slope and β_2 is the bias. We are going to match this model using various linear regression. For better dimensional data, the strategy works equally.

There we now have now it! That’s linear regression from scratch. I hope you really liked and realized one factor. I’d welcome any strategies and constructive criticism. Maintain tuned for my subsequent submit, the place I’ll cowl linear classification.

All the code is obtainable on github.